Seidel Aberration Imaging
Introduction
The purpose of this page is to demonstrate how the Seidel Aberrations affect image quality. Unlike the other parts of this website, this is an offline/noninteractive demonstration due to the immense processing power required to perform each simulation.
Method
The Seidel Aberrations are specified using three subscripts, where each subscript is the power of each of the wavefront power series expansion terms: $$W_{ijk} = H^{i}\rho ^{j}\cos ^{k}\theta$$ The image is generated using the superposition integral $$I(x,y) = \iint_{-\infty }^{\infty }G(x,y)\left | \Im^-1 (P(-\lambda zf_U, -\lambda z f_V)) \right |^2dxdy$$ where $P(-\lambda zf_U, -\lambda z f_V)$ is the pupil function $$P(x_p, y_p) = circ\left ( \frac{\sqrt{x_p^2 + y_p^2}}{r_{xp}} \right )e^{-ikW(x_p,y_p)}$$ and $G(x,y)$ is the ideal nonaberrated image. A simulation was performed for each of the first, third, and fifth order Seidel Aberrations. Each simulation contains three waves of the specified aberration. Simulations were performed on two images: the 1951 USAF Resolution Chart and the "Living Room" scene (a test image widely used throughout the history of image science).Optical System Parameters
For this offline demonstration, the following optical system parameters were specified:| Parameter | Value |
|---|---|
| Image plane side length | 1 $mm$ |
| Wavelength | 500 $nm$ |
| Exit pupil diameter | 20 $mm$ |
| Exit pupil to image distance | 100 $mm$ |
| FFT Size | 512x512 |
References:
1. Computational Fourier Optics by David Voelz, SPIE Press, 2011
2. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB by Jason D. Schmidt, SPIE Press, 2010
Results
Image Field
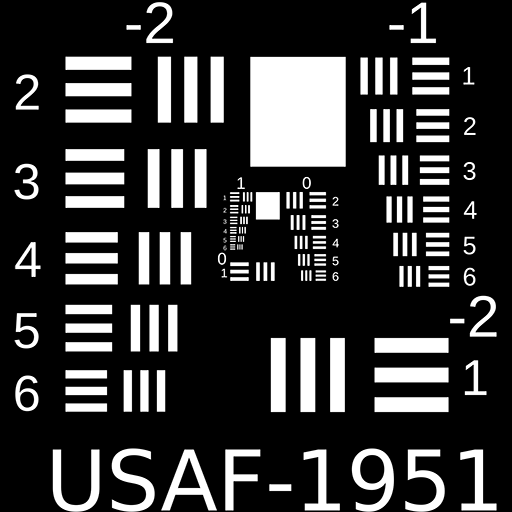

Diffraction Limited Image
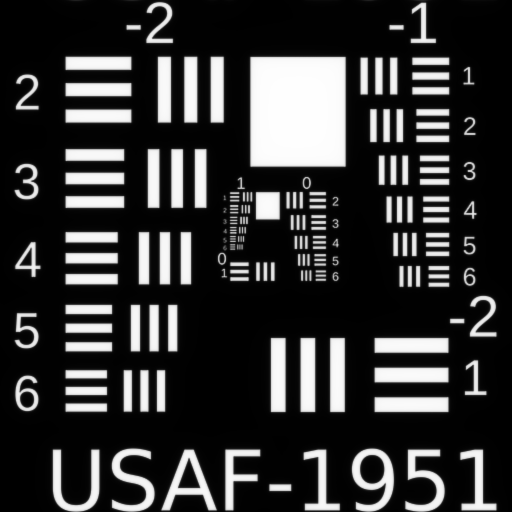

First Order Defocus $W_{020}$


First Order Tilt $W_{111}$
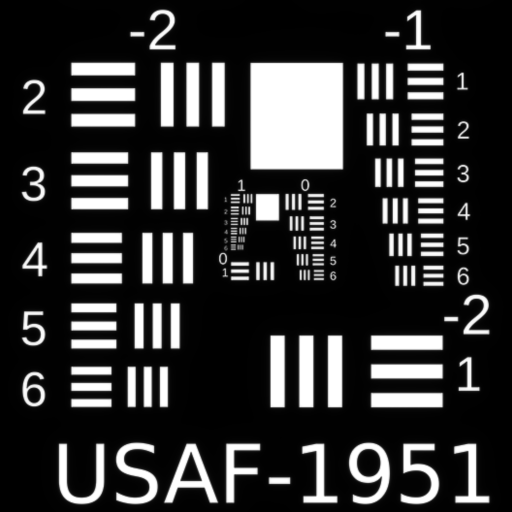

Third Order Spherical $W_{040}$
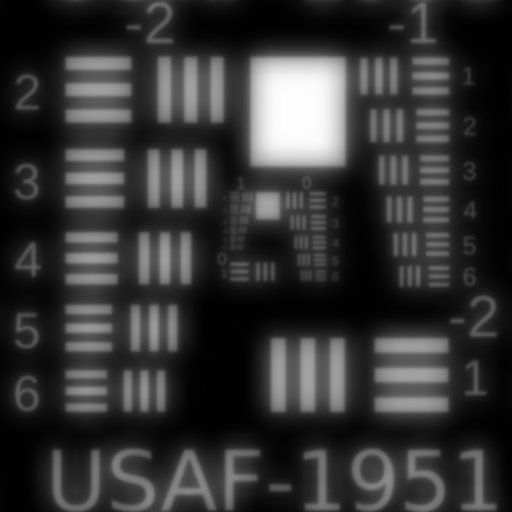

Third Order Coma $W_{131}$
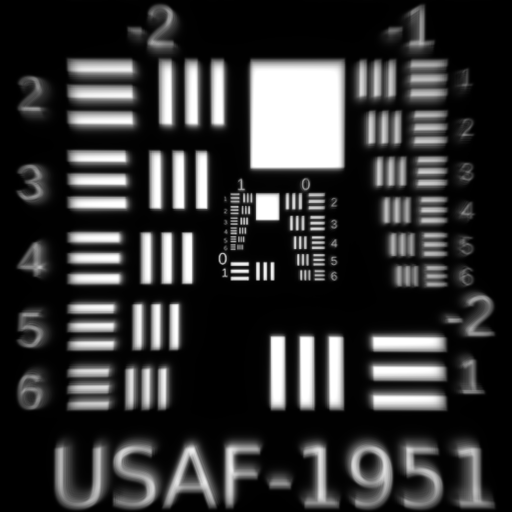

Third Order Astigmatism $W_{222}$


Third Order Field Curvature $W_{220}$


Third Order Distortion $W_{311}$
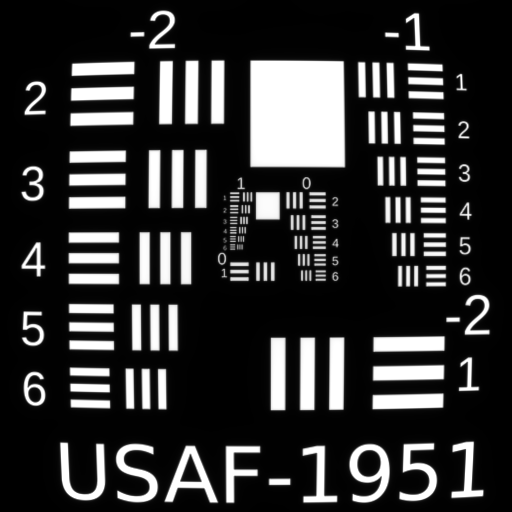

Fifth Order Spherical $W_{060}$


Fifth Order Sagittal Oblique Spherical $W_{240}$
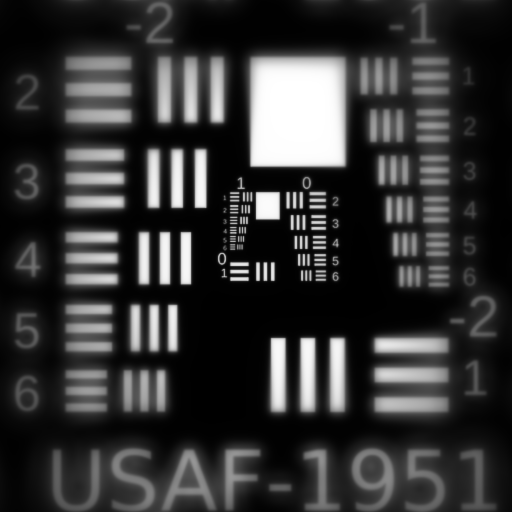

Fifth Order Field Curvature $W_{420}$


Fifth Order Linear Coma $W_{151}$
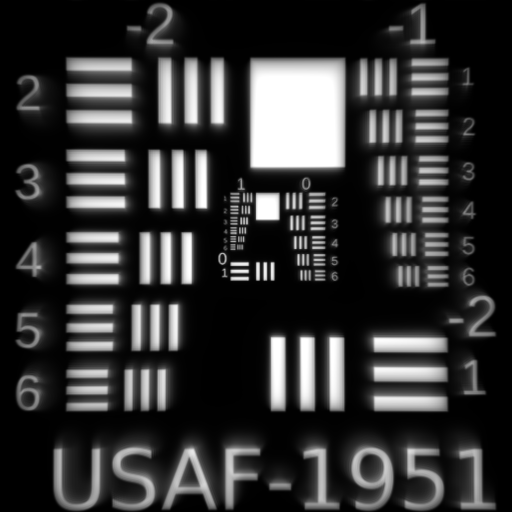

Fifth Order Cubic Coma $W_{331}$
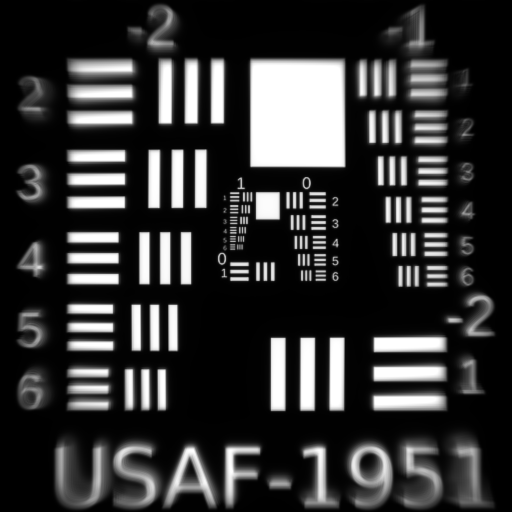

Fifth Order Distortion $W_{511}$
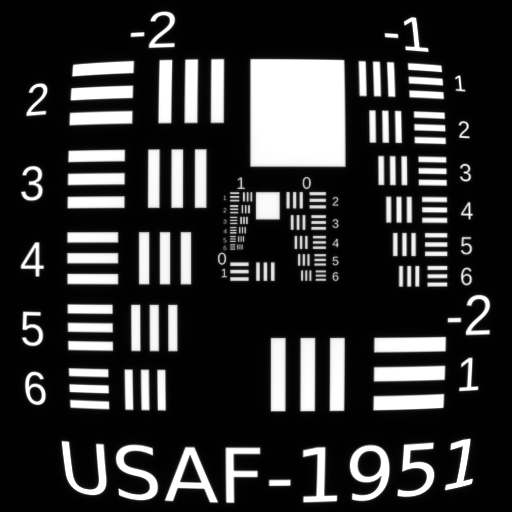

Fifth Order Tangential Oblique Spherical $W_{242}$
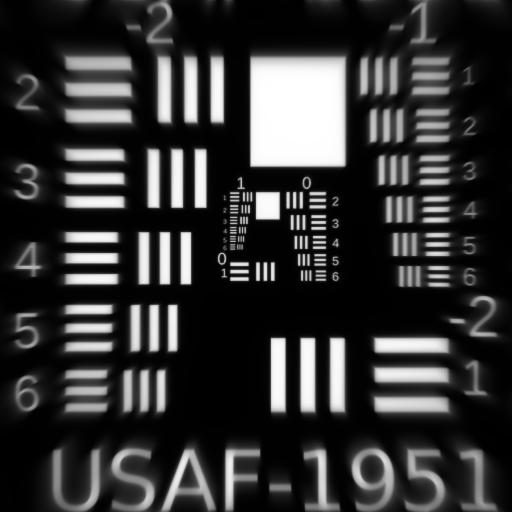

Fifth Order Astigmatism $W_{422}$


Fifth Order Line-Elliptical Coma $W_{333}$

